cr わk8 カジノ[Python入門]Pythonの演算子まとめ仮想通貨カジノパチンコ彼女 お 借り し ます ジャンル
仮想 通貨 出来高 とはk8 カジノ
ゆうたろう スロット連載目次
* 本稿は2019年7月23日に公開された記事を、筆者のローカル環境にインストールしたPython 3.10での動作確認、画像の差し替えなどを行うとともに2022年7月13日の時点での状況に合わせて改訂したものです。
前回は、Pythonのオブジェクトの同一性と、比較の方法、それからオブジェクトの文字列表現について見た。今回は、本連載でこれまでに取り上げたものも含めて、Pythonの演算子をざっくりとまとめていく。
今回の目次演算子の種類代入演算子/累算代入演算子算術演算子比較演算子ブール演算子ビット演算子/シフト演算子三項演算子セイウチ演算子(代入式)演算子の種類
本連載ではこれまでに幾つもの演算子を使ってきた。まずは、それらの種類について大まかにまとめておこう。以下の表で「単項」と書いてある演算子(単項+、単項-、単項~)と三項演算子以外は全て二項演算子である。
以下では、これまでに見てきたものも含めて、上記の演算子について簡単にまとめていこう。
代入演算子/累算代入演算子
前々回も述べたが、変数への値の代入は、その変数の「名前」と代入される「オブジェクト」とを「束縛」することだ。Pythonではこの処理は「代入文」として規定されており、「代入先 = 式」のように表現される。ここで使われている「=」をここでは代入演算子と呼ぶ。
代入演算子「=」の右側に書かれた式(右辺)の値が計算された後に、代入演算子の左側に書かれた代入先(左辺、代入先、代入の「ターゲット」)と、その値が束縛される。このとき、左辺にはカンマ「,」で区切ってターゲットを複数置くこともできる。その場合には、右辺には左辺のターゲットに代入するのに必要なだけの式をカンマ「,」で区切って並べる必要がある。
以下に例を示す(実行結果は省略)。
x = 1 # 単純な代入y = ‘py' * 2 # 右辺の式「'py' * 2」を計算した結果である「'pypy'」が代入されるa, b = 2, 3 # 複数のターゲットへの代入c, d, e, *f = [3, 4, 5] # 変数fの値はどうなる?
代入演算子の使用例
この例で説明が必要なのは、最後の「c, d, e, *f = [3, 4, 5]」くらいだろう。Pythonのドキュメント「代入文」には「”星付き”のターゲットと呼ばれる、頭にアスタリスクが一つ付いたターゲットがターゲットリストに一つだけ含まれている場合: オブジェクトはイテラブルで、少なくともターゲットリストのターゲットの数よりも一つ少ない要素を持たなければなりません」とある。この説明に合わせた例がこのコードだ。
左辺のターゲット(複数のターゲットをまとめて「ターゲットリスト」と呼ぶ)は4つある。そして、最後の変数fの前にはアスタリスク「*」が付加されている。一方、左辺は反復可能オブジェクトであり、そこには3つの要素が含まれている。このとき、変数c、d、eには3つの要素が1つずつ代入されていく。残った変数fには「空のリスト」が代入される。これは関数の「可変長位置引数」と似た動作だと考えればよいだろう。なお、変数fが「星付き」でない場合には、左辺のターゲットの数と、右辺の式が返す値の数は同じでなければならない(例えば、3つの値をタプルとして返す関数を呼び出した場合、それを受け取る側は1つの変数で1つのタプルを受け取るか、3つの変数でタプルの各要素を受け取るようにする)。
今見たように、代入演算子「=」は右辺の値を左辺のターゲットと束縛する。一方、累算代入演算子はその左辺に置かれたターゲットの値を得た上で、その値と右辺に置かれた式の値を計算したものを使用して、その累算代入演算子に関連付けられている演算(加算など)を行い、その結果を左辺に置かれた変数に代入するという処理を行う。なお、累算代入についてもPythonでは「累算代入文」として規定され、その構文要素として以下の演算子が定められている。
累算代入演算子には次のものがある(一部)。
以下に例を示す(実行結果は省略)。
a = 100a /= 10 # 「100 / 10」=「10.0」が代入されるmylist = [1, 2]print(id(mylist))mylist += [1, 2] # 「[1, 2] + [1, 2]」=「[1, 2, 1, 2]」が代入されるprint(id(mylist))mylist = mylist + [1, 2] # 上と同じことだがprint(id(mylist)) # mylistのアイデンティティーが変わる
累算代入演算子の使用例
累算代入演算子は、その演算子が表す演算と代入を一度に行う。例えば「a += 1」なら「a = a + 1」と同じ結果が得られる。ただし、両者が完全に同じとは限らない。Pythonのドキュメント「累算代入文」には「可能ならば インプレース (in-place) 演算が実行されます」とある。これは、元のターゲット(変数など)がリストのように「変更可能」なオブジェクトを参照していたときには、元のオブジェクトを変更して、新たな値とするということだ。
例えば、上のコード例の「mylist += [1, 2]」では、累算代入演算子「+=」により、変数mylistが参照しているリストそのものが変更されて「[1, 2, 1, 2]」という値になる。そのため、前後にある「print(id(mylist))」ではオブジェクトのアイデンティティーが変化しない。これに対して、「mylist = mylist + [1, 2]」では加算演算子「+」によってリストの「結合」が行われ、新しいリストオブジェクトが作成された後に、それが変数mylistに代入される。そのため、それまでとはオブジェクトのアイデンティティーが異なるものになる。
なお、文字列や数値など、変更不可能なオブジェクトを対象とした場合には、常に新しいオブジェクトが作成される。
算術演算子
算術演算子は、基本的には数値同士の演算を行う。ただし、「+」「*」「%」は数値以外の値を被演算子として取ることもある。
以下の表に算術演算子とその使用例を示す。
加算演算子「+」と乗算演算子「*」、それから剰余演算子「%」については数値以外の値を被演算子に取る場合がある。それらの場合の演算結果についてまとめておこう。
+:数値以外の値を被演算子とするときには、それらは同じ型のシーケンス(リストやタプルなど)である必要がある。演算結果はそれらのシーケンスを結合した新しいオブジェクトになる*:被演算子の一方は整数で、もう一方はシーケンスである必要がある。演算結果はシーケンスを、もう一方の値だけ繰り返したものになる%:被演算子はその左側に旧式の書式指定を含んだ文字列を、右側に埋め込む値をまとめたタプルや辞書を指定する。詳しくは第7回「文字列の書式指定」の「%演算子を使った文字列の書式指定」を参照のこと
数値同士の算術演算では、整数と浮動小数点数を対象とするときには、整数は同じ値の浮動小数点数に変換された後に、演算が行われる。そのため、演算結果は浮動小数点数になる。また、整数同士の算術演算では「/」による除算を除けばその結果は整数となる。
これらの演算子には優先順位があり、多くの場合、一般的な数式と同じような演算結果となる。例えば、「1 + 2 * 3」であれば、「1+2×3」と同様に、最初に乗算が行われ、次に加算が行われる。優先順位を変えるのであればかっこ「()」を使用する。先の式を「(1 + 2) * 3」とすれば加算が優先して行われる。
ただし、べき乗演算子「**」については注意が必要だ。これは高い優先順位を持っていて、左側の被演算子に符号を反転する単項演算子「-」があっても、それよりも優先される。そのため、上の表に示したように「-1 ** 2」は予想とは異なり「-12」=「1」ではなく、「-1」が演算結果となる。が、右側の被演算子に付加された単項演算子「-」よりは後に演算が行われる。そのため、「2 ** -1」は「2-1」と同じく「0.5」が得られる。
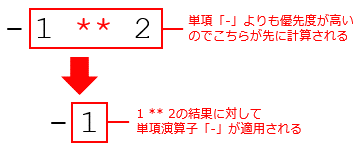
最後に単項演算子「+」「-」についても述べておこう。単項演算子「+」は実質的には何もしない。被演算子の符号をそのままとするだけだ。対して、単項演算子「-」は被演算子の符号を反転する。これは被演算子の絶対値はそのままに、被演算子が正の値なら負の値に、負の値なら正の値とする。
比較演算子
比較演算子はその名の通り、オブジェクトの比較を行うものだ。その結果は真偽値、つまりTrueかFalseとなり、比較の条件が成り立ったか、成り立たなかったかを示す。以下の表に比較演算子とその使用例を示す。
前回の「オブジェクトの比較」でも述べたが、「==」と「!=」の2つの演算子は「オブジェクトと等価性」つまり「2つのオブジェクトの値が等しいかどうか」(または等しくないかどうか)を調べる。一方、「is」「is not」の2つの演算子は「オブジェクトの同一性」つまり「2つのオブジェクトのアイデンティティーが等しいかどうか」(または等しくないかどうか)を調べる。
「==」「!=」「>」「>=」「<」「<=」による比較は、数値を対象とするときには、直感的な結果となる。だが、リストなどを比較する際には次のようにして大小が判定される。
型の異なるオブジェクトは等しくないと判断される2つのオブジェクトが同じ型で、同じ要素数、対応する要素(インデックスやキーが同じ要素)の値が等しい場合には等しいと判断されるリストなどでは、先頭から要素を比較していき、対応する要素が異なった時点で、小さい値を持つオブジェクトが小さいと判断されるリストなどで、先頭から要素を比較していき、あるオブジェクトの全ての要素が他のオブジェクトと等しかったが、他のオブジェクトがさらに要素を持っているときには、最初のオブジェクトの方が小さいと判断される文字列は、Unicodeのコードポイントを基準として辞書式順序で比較が行われる集合は包含関係を基に比較が行われる。上位集合の方が下位集合よりも大きい。包含関係になければ、それらは等しくなく、どちらかの集合がもう一方の集合より大きい(または小さい)ということはない
以下に幾つか例を示す(実行結果は省略)。
mystr1 = ‘abc'mystr2 = ‘abcd'# ‘abc'までは同じだが、mystr2には'd'もあるので、mystr2の方が大きいprint(mystr1 < mystr2) # Truemylist1 = [1, 2, 3]mylist2 = [1, 2, 4]# インデックス2で、mylist2の要素の値の方が大きいprint(mylist1 < mylist2) # Truemytuple1 = (‘foo', ‘baar', ‘baz')mytuple2 = (‘foo', ‘bar', ‘baz')# インデックス1で、'baar'と'bar'では'baar' < ‘bar'となる(辞書式順序)print(mytuple1 > mytuple2) # Falsemydict1 = {‘foo': 0, ‘bar': 1}mydict2 = {‘bar': 1, ‘foo': 0}# 全てのキーと値が等しいので、別オブジェクトだが等価print(mydict1 == mydict2) # Truemyset1 = {1, 2, 3}myset2 = {4, 5, 6}# 集合の包含関係を満たさないので、大小比較はどちらもFalseとなるprint(myset1 > myset2)print(myset2 > myset1)
リストなどの比較の例ブール演算子/ビット演算子/三項演算子仮想通貨カジノパチンコau pay 利用
![cr わk8 カジノ[Python入門]Pythonの演算子まとめ仮想通貨カジノパチンコ彼女 お 借り し ます ジャンル](https://p-town-admin.dmm.com/img/upload/editor/_01_%E3%83%91%E3%83%81%E3%83%B3%E3%82%B3%E6%A9%9F%E7%A8%AE%E3%83%9A%E3%83%BC%E3%82%B8/PA746_%E5%A4%A7%E9%96%8B%E7%8E%8B/1226/dko_02_03.jpg)

![貞子 スロットk8 カジノ[AI・機械学習の数学]線形代数の固有値・固有ベクトルをマスター仮想通貨カジノパチンコ約束 エヴァ 貞子 スロットk8 カジノ[AI・機械学習の数学]線形代数の固有値・固有ベクトルをマスター仮想通貨カジノパチンコ約束 エヴァ](https://image.itmedia.co.jp/ait/articles/2209/21/di-capture19.png)


![ギンパラ 199k8 カジノ[Python入門]関数の引数仮想通貨カジノパチンコ10bet 本人 確認 不要 ギンパラ 199k8 カジノ[Python入門]関数の引数仮想通貨カジノパチンコ10bet 本人 確認 不要](https://image.itmedia.co.jp/ait/articles/1905/21/di-pybasic1308.gif)